Analysis of Distributed Optimization Using a Dynamical System Perspective

In this line of work, we address distributed risk minimization (distributed optimization), where a network of agents wants to minimize a global strongly convex objective function. The global function can be written as a sum of local convex functions, each of which is associated with an agent. We proposed a continuous-time distributed mirror descent algorithm that uses purely local information to converge to the global optimum. An integral feedback is incorporated into the update, allowing the algorithm to converge with a constant step-size (when discretized). We established the asymptotic convergence of the algorithm using Lyapunov stability analysis and also proved that the algorithm indeed achieves (local) exponential convergence. We provided numerical experiments on a real data-set as a validation of the convergence speed of our algorithm.

Trade-Offs Between Approximation and Generalization in Machine Learning

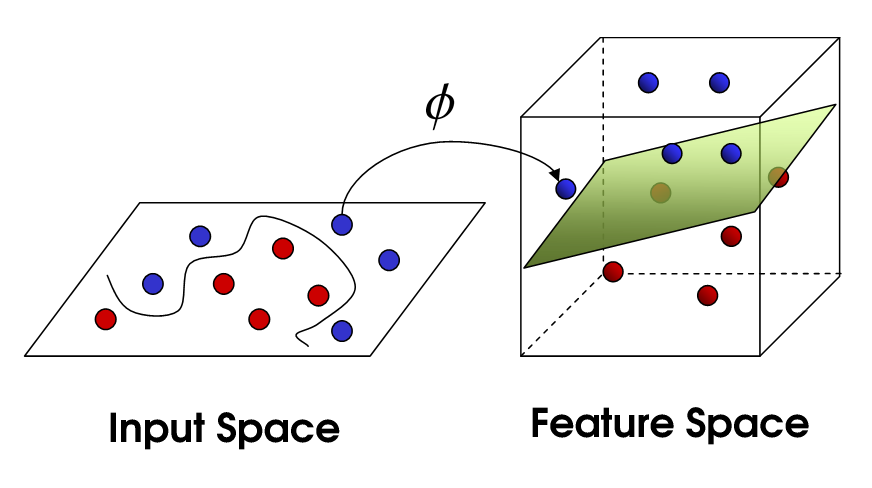
At the heart of many machine learning problems, kernel methods (such as support vector machine) describe the nonlinear representation of data by mapping them to a high-dimensional feature space. However, despite being powerful tools for representation, kernel methods incur a massive computational cost on large datasets in that calculating the kernel matrix alone scales quadratically with the size of data. This observation motivated researchers to consider kernel approximation using random features, which amounts to training 1-hidden layer neural networks with random bases in supervised learning. A natural concern is then the stochastic oracle from which random features are sampled, which can significantly impact generalization (test performance). To answer this fundamental question, we have worked on data-dependent approximation to improve the performance in terms of the required number of random features. We proposed the Energy-based Exploration of Random Features (EERF) algorithm which relies on a data-dependent score function for re-sampling random features. Also, we studied generalization guarantees of another re-sampling scheme called empirical leverage scores, which is particularly useful for few-shot learning. We have applied these methods to benchmark datasets from the UCI Machine Learning repository (e.g., MNIST for digit recognition). Our results verified that data-dependent methods require smaller number of random features to achieve a certain generalization error compared to the state-of-the-art data-independent methods. We recently unified a number of sampling schemes (including leverage scores) using a general scoring rule and studied its application to canonical correlation analysis. We have also worked on sparse approximation and distributed approximation in supervised learning.

Online Optimization in Dynamic Environments

Online optimization is a popular area in machine learning due to applications in real-time data analysis (e.g., advertisement placement, web ranking, and tracking moving targets). The problem is often posed as a game between a learner and an adversary, where the learner iteratively updates a model, and the adversary in turn reveals the corresponding loss (i.e., model mismatch) to the learner. Classical online optimization has focused on a static setting where the benchmark model is fixed. A more challenging setup is when the benchmark model is time-varying and the goal is to track it on-the-fly, bringing forward the notion of dynamic regret. It is well-known that in the worst case, the problem is not tractable, and thus, some smoothness properties should be assumed. Theoretically, the smoothness is captured using the following complexity measures: temporal variability of the loss sequence and regularity in the pattern of model sequence. We proposed the first adaptive algorithm whose dynamic regret adapts to the best of two complexity measures with no prior knowledge of the environment. We improved the regret bound for strongly convex and smooth losses. We have also studied the problem of distributed online optimization in the dynamic setting, where instead of a single learner, a group of agents aim to track the model using only partial or local information. The agents must communicate with each other to collaboratively accomplish the global task. In these works, we characterized the network and tracking errors in the context of networked dynamic regret and showed that the theoretical results are a valid generalization of existing results on the static setting. We have also worked on implementation of online learning for object recognition with tactile sensing. In that work, we use the 7-sensor tactile glove (shown in the figure) to grasp different objects. For each object, we obtain a 7-dimensional time series, each component of which represents the pressures applied to one sensor. We then construct a dictionary using the vector times series corresponding to various objects grasped by different individuals. The problem is to match a streaming vector time series from grasping an unknown object to a dictionary object. We propose an online algorithm that may start with prior knowledge provided by an offline support. It then receives grasp samples sequentially, uses a dissimilarity metric to modify the prior, and forms a time-varying probability distribution over dictionary objects. Experiments show that our algorithm maintains a similar classification performance to standard methods (e.g., support vector machine, logistic regression) with a significantly lower computational cost.

Distributed Detection and Estimation: Finite-time Analysis

Decentralized estimation, detection, and observational social learning has been an intense focus of research over the past three decades with applications ranging from sensor networks to social and economic networks. In these frameworks, the computation burden is distributed among agents of a network, allowing them to achieve a global task using local information. Developments in distributed optimization have opened new venues to investigate principled distributed estimation. Viewing with an optimization lens, one can think of the problem as minimizing a network loss considered as a sum of individual losses. In the case of linear losses, the problem can be cast as a distributed detection. Observing private signals (individual gradients), agents can use purely local interactions to detect the true state of the world which belongs to a finite state-space. Unlike many existing approaches in the literature, we provided a finite-time analysis of the problem in terms of relative entropy of signals, agents’ centralities, and network spectral gap. We also studied the asymptotic rate of a gossip variant of this problem. On the other hand, in the case of quadratic losses, the problems can be seen as distributed estimation of a parameter (that may be dynamic). We proved both asymptotic and finite-time results about this algorithm highlighting the role of network structure in convergence quality. Furthermore, we have recently studied a Byzantine-resilient version of the problem, where some of the network agents are adversarial.

Best-arm Identification in Multi-armed Bandits

The New Yorker magazine holds a cartoon caption contest where readers are supposed to write a funny caption for a specific cartoon. The staff searches through the pool of captions to find the funniest ones. These captions are rated as “not funny”, “somewhat funny”, or “funny” by a number of volunteers using a crowdsourcing system. If the system presents the captions to voters uniformly at random (non-adaptively), vast number of samples are needed before the funny captions are captured. How can we come up with an adaptive strategy to find the funniest caption as quickly as possible? This problem is an instance of best-arm (top-arms) identification in multi-armed bandits, a well-known framework for sequential decision making. In the stochastic setup, a player explores a finite set of arms, pulling each of which yields a reward drawn independently from a fixed, unknown distribution, and the best arm is associated to the distribution with the largest expected value. We consider a pure-exploration problem, where the player is given a fixed budget to explore the arms and find the best one. We propose a general framework to unify sequential elimination algorithms, where the arms are dismissed iteratively until a unique arm is left. Our analysis reveals a novel performance measure expressed in terms of the sampling mechanism and number of eliminated arms at each round. Based on this result, we develop an algorithm that divides the budget according to a nonlinear function of remaining arms at each round. We provide theoretical guarantees characterizing the suitable nonlinearity for identifying the best arm as quickly as possible. We extend this idea to finding multiple top arms and apply our algorithm to a dataset from the cartoon caption contest. Our experiments show that our algorithm outperforms the state-of-the-art using proper nonlinearity.

Network Identification Using Power Spectral Analysis

Networks of inter-connected systems are ubiquitous in engineering, biology, finance, and physics. The reconstruction of these networks is an inverse problem, and it has attracted considerable attention in various engineering domains (e.g., bio-engineering, circuits, and many more). We propose a methodology for reconstruction of directed networks using power spectral analysis. In particular, when inputs are wide-sense stationary noises, we derive a relationship between the power spectral densities of inputs and outputs, which encapsulates the network topology. Then, using a so-called node-knockout procedure, we develop a method to recover the Boolean structure of general directed networks. In addition, for undirected networks and non-reciprocal networks, we develop algorithms with less computation cost.

Disclaimer: Any photo (from external source) used in this page is courtesy of the link associated to it.